Relatório TP-1

Este trabalho consistiu da construção e análise de um robô diferencial utilizando controle proporcional derivativo. O robô foi construído com peças Lego, motores elétricos e sensores shaft encoders. O objetivo prático do robô é marcar sua trajetória em uma superfície e realizar três quadrados (de lado 30 cm) consecutivos e três círculos (de raio 30 cm) consecutivos.

Nosso objetivo foi montar um robô que fosse leve e pequeno, mas que suportaria o peso e tamanho da HandyBoard. Optamos também por não utilizar uma roda Roll-On pois queríamos que nossa montagem tivesse apenas peças Lego. Como consequência, optamos por utilizar uma roda livre, similar a de carrinhos de supermercado, que se adapta bem à mudanças de direções.

O robô possui 2 motores Pololu (35:1 Metal Gearmotor 15.5Dx30L mm), 2 shaft encoders (1 para cada motor) e 1 HandyBoard além de 1 marcador (caneta para marcar CDs) e diversas peças Lego. Suas dimensões estão descritas abaixo.

Altura: 15,0cm; Comprimento: 18,0cm; Largura: 13,0cm; Eixo traseiro: 9,0cm; Distância entre eixos: 14,0cm; Diâmetro rodas traseiras: 4,5cm; Diâmetro roda dianteira: 2,5cm.

Os motores foram montados na parte dianteira do robô e seus eixos possuem, cada um, uma polia com 6 furos, para a montagem dos shaft encoders, e uma rosca sem fim para transmitir a tração para as rodas traseiras. A transmissão é feita com uma coroa de 24 dentes. Conforme mostrado na figura abaixo:

Cada shaft encoder foi preso às peças Lego por meio de 2 elásticos. Para que a montagem ficasse segura, foi necessário que as peças Lego, amarradas ao shaft encoder, ficassem de cabeça para baixo em relação a estrutura do robô. Para inverter essas peças utilizamos peças no formato 'L' com dobradiças nas laterais do robô. Veja a montagem na figura abaixo:

Para a roda dianteira montamos uma biruta - uma espécie de roda que pode girar livremente em qualquer direção no plano da superfície. Optamos por montar essa roda pois ela não deveria atrapalhar os movimentos do robô. No entanto, testes posteriores mostraram que esse tipo de roda provocava um pequeno desvio nas mudanças de direção do robô.

Como parte da especificação do trabalho, o robô deveria ser capaz de marcar sua trajetória em uma cartolina, papel kraft etc. Para isto testamos 3 tipos de marcadores: lápis, caneta, caneta para marcar CDs; e 2 tipos de presilhas: borracha, abraçadeira de nylon. O marcador é preso na parte anterior do robô.

Um teste inicial usando lápis e abraçadeira de nylon mostrou que, por estar muito próximo ao eixo das rodas que recebem torque do motor, parte da tração é perdida quando o lápis apoia parte do robô. Por outro lado, se o lápis não estiver apoiado, dificilmente marca a superfície. Um segundo teste utilizando caneta e abraçadeira de nylon mostrou o mesmo problema. Utilizando agora caneta e borracha, notamos que a caneta adquire certa liberdade e perde constantemente sua posição marcando traçados aleatórios. Um último teste utilizando abraçadeiras de nylon e caneta para marcar CDs não mostrou perda de tração significativa sendo a opção escolhida.

O controlador utilizado é um microcontrolador HandyBoard de propósito geral. A HandyBoard foi colocada sobre o robô, sustentada por uma peça chapada de Lego montada acima dos shaft encoders. 4 colunas (traseira, dianteira, direita e esquerda) fazem o suporte da estrutura que contém ainda 1 parede traseira e 3 peças em L que evitam que a HandyBoard deslize sobre a estrutura. Um possível melhoria seria utilizar uma fita dupla face 3M para fixar melhor a HandyBoard.

Conforme especificado, o robô foi construído para realizar 3 quadrados consecutivos e 3 círculos consecutivos.

A princípio, a trajetória em quadrado parece simples. Porém, é preciso controlar o movimento retilíneo do robô e ainda ajustar os desvios de trajetória causados pela roda livre durante as curvas. O controle do movimento retilíneo foi feito com um controle proporcional e os desvios causados pela roda livre foram calibrados empiricamente.

O circulo foi feito atuando com velocidades diferentes nas rodas. O cálculo da potência de cada roda é feito pela formula:

R = L/2 (Pr + Pl)/(Pr - Pl)

Onde R é o raio da circunferência, L é o eixo traseiro, e Pr e Pl são as potências das rodas direita e esquerda, respectivamente. Para a circunferência de 30cm de raio para o lado esquerdo, a razão de velocidades entre a roda direita e esquerda foi de 55%. Ou seja, utilizamos, aproximadamente, a potência 25 na roda esquerda e de 40 na roda direita.

Utilizando o robô montado, fizemos um pequeno programa para extrair dados sobre um simples controle PD. O código a seguir trata do armazenamento dos dados e do controle PD.

void fwd(int power, int pgain, int dgain){
    int c = 0;
    int last_power = power;
    motor(1, power);
    while(!stop_button()){
 
        sleep(0.1);
        power += (encoder0_velocity - encoder1_velocity) * pgain - (power - last_power) * dgain;
        if( c < 100 ){
            dencoder[c] = (encoder0_velocity - encoder1_velocity);
            dpower[c] = power;
            velocity[c] = encoder0_velocity;
            c++;
        }
        if( power < 0 )
          power = 0;
        motor(1, power);        
    }
}

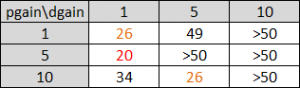
Escolhemos então 3 valores para os parâmetros dgain e pgain: 1, 5 e 10. As nove combinações possíveis foram então testadas e resumidas na tabela abaixo. Os valores da tabela indicam a iteração em que count e power estabilizaram para 100 e 0, respectivamente. O melhor resultado (destacado em vermelho na tabela) e o segundo melhor resultado (destacado em alaranjado) foram utilizados para gerar gráficos de iterações por power e iterações por counts.

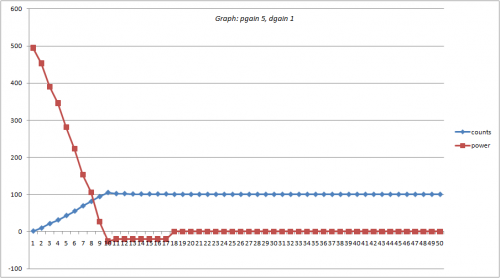
Melhor Resultado (dgain = 5, pgain = 1)

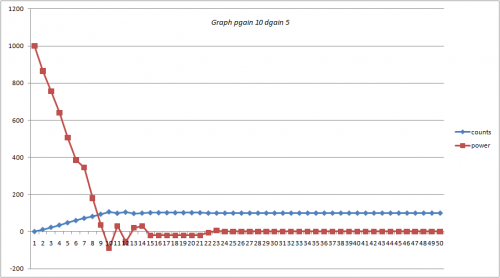
Segundo melhor Resultado (dgain = 10, pgain = 5)

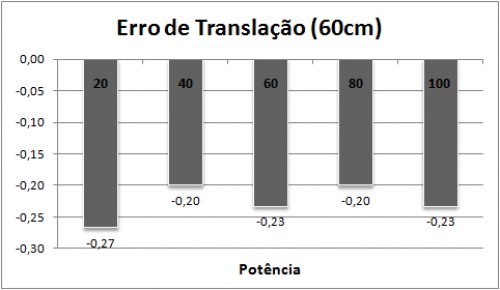
O calculo da distância é feito com base no número de rotações dos motores. Montamos os shaft encoders em polias com 6 furos, o que resulta em 12 pulsos em uma rotação completa dessa roda. Como há uma redução de 1/24 na transmissão do robô, então para uma rotação da roda traseira, são necessários 288 pulsos. Sendo assim sabemos que o robô precisa de 288 pulsos para andar 14,14cm (circunferência da roda traseira). Para outras distâncias, calculamos a proporção desse valor. Medimos o erro de translação para diferentes potências dos motores em uma trajetória retilínea de 60cm.

Como podemos perceber pela análise do gráfico, o erro foi mínimo (de aproximadamente -2 mm) para todas as potências. Podemos inferir também que o erro não foi dependente da potência escolhida, como podemos perceber pelos resultados aleatórios do gráfico.

A rotação é feita girando as rodas traseiras em sentidos opostos. O cálculo do ângulo de rotação é feito com base nas medidas dos shaft encoders. Sabemos que são precisos 144 pulsos para robô girar 90º.

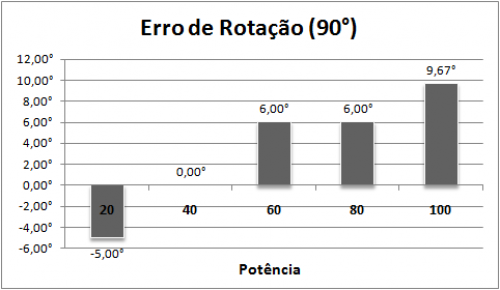
Medimos o erro de rotação para diferentes potências do motor para uma rotação de 90º.

Conforme podemos perceber o erro de rotação cresce linearmente com o aumento de potência. Devido ao desvio provocado pela roda dianteira, na tarefa do quadrado, fazemos uma rotação ligeiramente menor que 90° para corrigir a trajetória.

As trajetórias (quadrada e circular) foram testadas diversas vezes e apresentadas no dia 5 de setembro ao monitor e professor do curso.

Neste trabalho desenvolvemos e implementamos um robô diferencial com controle proporcional derivativo. Descrevemos algumas formas de montar o robô e alguns problemas associados a estas montagens. Uma vez o robô pronto, testamos vários parâmetros de controle até que o robô conseguisse realizar trajetórias quadradas e circulares previstas na especificação do problema, com certa precisão.

Wikipedia contributors, 'PID controller', Wikipedia, The Free Encyclopedia, <http://en.wikipedia.org/w/index.php?title=PID_controller&oldid=450062751> [accessed 02 September 2011]

Robotic Explorations: An Introduction to Engineering Through Design. Martin, F. G., Prentice Hall; ISBN: 0-130-89568-7.

#include "fencdr0.icb"
#include "fencdr1.icb"
 
#define FD 1
#define BK -1
#define POTENCIA0 40
#define POTENCIA1 40
#define POTENCIA90 50
#define PULSOSVOLTA 298.0 //288
#define DIREITO 0
#define ESQUERDO 1
 
 
/* 	Calcula o número de pulsos necessários medidos pelos shaft encoders para 
realizar uma trajetória retilínea em uma certa distancia
	Parâmetro:
		distancia: distância em centimetros
*/
int CalcPulsos(float distancia);
 
 
/* 
	Faz um movimento retilínio dependente da direção e distância
	Parâmetros:
		direcao - direção do movimento do robô. 1 = para frente; -1 = para trás;		
		distancia - distância a ser percorrida em centimetros;	
*/
void Anda(int direcao, int pulsos);
 
 
/* 	Monitora e controla as velocidades de cada motor em paralelo com a função Anda
	Parâmetro:
		direcao: direção do movimento do robô. 1 = para frente; -1 = para trás;
*/
void controle(int direcao);
 
 
/* 	Faz uma curva de 90° com o robô 
	Parâmetro:
		lado: direção do movimento do robô. 0 = direito; 1 = esquerdo;
*/
void Curva90(int lado);
 
 
/* 
	Faz um quadrado completo
	Parâmetros:
		distancia - tamanho do lado do quadrado em centimetros;
		lado - direção do movimento do robô. 0 = direito; 1 = esquerdo;		
*/
void Quadrado(float distancia, int lado);
 
 
/* Faz um circulo completo de 30cm de raio */
void Circulo();
 
 
void main()
{
    int modo = 1;
    printf(" press stop to change [circle]\n");
    while(1){
        if(start_button()){        
            sleep(0.2);
            while(start_button());
            printf("Running!\n");
            if(modo == 1){
                Circulo();
                Circulo();
                Circulo();
                printf(" press stop to change [circle]\n");
            }
            else{
                Quadrado(32.0, ESQUERDO);
                Quadrado(32.0, ESQUERDO);
                Quadrado(32.0, ESQUERDO);
                printf(" press stop to change [square]\n");
            }
        }
        if(stop_button()){
            sleep(0.2);
            while(stop_button());
            modo = (modo + 1) % 2;
            if(modo == 1){
                printf(" press stop to change [circle]\n");
            }
            else{
                printf(" press stop to change [square]\n");
            }
        }
    }
}
 
int CalcPulsos(float distancia)
{
	//14.1371 é o tamanho da circunferência das rodas traseiras    
	return (int)(distancia/14.1371 * PULSOSVOLTA);
}
 
void Anda(int direcao, int pulsos)
{
    int break0=1, break1=1;    
    int pid;
    sleep(0.5);
    encoder0_counts = 0;
    encoder1_counts = 0;
    motor(0, direcao*POTENCIA0);
    motor(1, direcao*POTENCIA1);
    pid = start_process(controle(direcao));
    while(break0 || break1){                      
        if(encoder0_counts >= pulsos){
            off(0);
            break0=0;
        }
        if(encoder1_counts >= pulsos){
            kill_process(pid);
            off(1);
            break1=0;
        }                  
    }
}
 
void controle(int direcao)
{
    int pwr = 0;
    while(1){
        if(encoder0_velocity > encoder1_velocity){
            pwr += 1;        
        }
        else if(encoder0_velocity < encoder1_velocity){
            pwr -= 1;          
        }
        if(POTENCIA1 + pwr > 100)
            motor(0, direcao*(POTENCIA0 - pwr));
        else
            motor(1, direcao*(POTENCIA1 + pwr));    
 
        sleep(0.1);        
    }
}
 
void Curva90(int lado)
{
    int break0=1, break1=1;
    sleep(0.5);
    encoder0_counts = 0;
    encoder1_counts = 0;
 
    if(lado == ESQUERDO){
        motor(0, BK*POTENCIA90);
        motor(1, FD*POTENCIA90);        
    }
    else{
        motor(0, FD*POTENCIA90);
        motor(1, BK*POTENCIA90);
    } 
 
    while(break0 || break1){                 
        if(encoder0_counts >= (int)PULSOSVOLTA/2-24){ 
            off(0);
            break0=0;
        }
        if(encoder1_counts >= (int)PULSOSVOLTA/2-24){
            off(1);
            break1=0;
        }                  
    }
}
 
void Quadrado(float distancia, int lado)
{
    Anda(FD, CalcPulsos(distancia));
    Curva90(lado);
    Anda(FD, CalcPulsos(distancia));
    Curva90(lado);
    Anda(FD, CalcPulsos(distancia));
    Curva90(lado);
    Anda(FD, CalcPulsos(distancia));
    Curva90(lado);
}
 
void Circulo()
{
    int pid;
    int pwr0 = 25;
    int pwr1 = 40;
    sleep(0.5);
    encoder0_counts = 0;
    encoder1_counts = 0;
 
	//Liga Motores
	motor(0, pwr0);
    motor(1, pwr1);
 
	while(1){      
		//Monitora e controla a velocidade de cada motor        
		if(encoder0_velocity > 10) pwr0--;
        else if(encoder0_velocity < 10) pwr0++;
        if(encoder1_velocity > 13) pwr1--;
        else if(encoder1_velocity < 13) pwr1++;
 
        motor(0, pwr0);
        motor(1, pwr1);
 
		//Desliga motores ao terminar o circulo        
		if(encoder0_counts >= CalcPulsos(178.0) || encoder1_counts >= CalcPulsos(240.0)){
            off(0);
            off(1);            
            break;
        }
        sleep(0.1);
    }
}