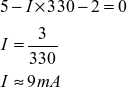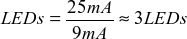Trabalho Prático III

Tarefa 1:

Seção 3.6.5 Exercícios

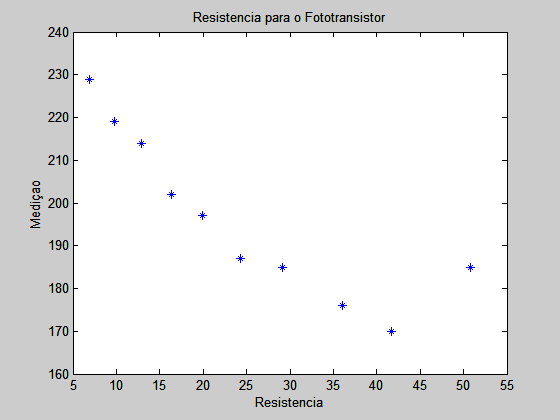
1 – Após montar o circuito proposto pelo exercício, colocamos o sensor virado para uma superfície branca a uma distância constante. Variando o valor da resistência, pudemos notar diferentes leituras do sensor. O melhor valor de resistência é aquele que provê a maior sensibilidade para o fototransistor, portanto, no nosso experimento, é a resistência associada ao menor valor lido pelo sensor. Utilizando um potenciômetro de 47K ohms de resistência e a montagem da figura 3.51 o gráfico 1 foi obtida pela variação da resistência do potenciômetro.

Gráfico 1

No gráfico o melhor valor para a resistência é de cerca de 43K ohms, valor muito próximo aos 47K fornecidos pelo sensor da HandyBoard.

2 - a)

b) Como o 68HC11 tem capacidade de fornecer em torno de 25mA e cada LED consome por volta de 9mA, o total de LEDs que pode ser conectado é:

Tarefa 2:

Seção 5.1.3 Exercícios

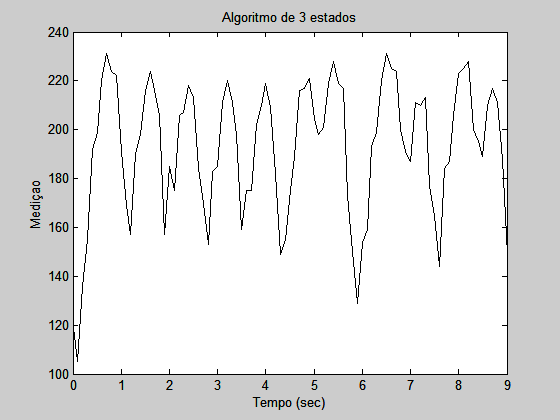
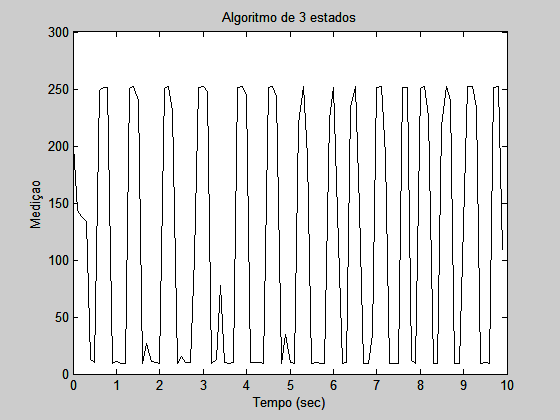
1 - O sensor óptico foi posicionado do lado direito do robô. A função calibrate() define o inner goal e outer goal. No programa, quando o robô está longe da parede (valor do sensor maior que o outer goal) ocorre a chamada da função right() corrigindo a velocidade das rodas do robô, fazendo com que ele vire em direção a parede. Quando o valor do sensor é menor que o inner goal o inverso acontece, usando-se a função left(). A função de seguir em linha reta, straight() é chamada quando a medição do sensor esta entre os goals. Os gráfico 2 e 3 mostram o desempenho do algoritmo seguidor de parede de três estados para duas situações diferentes.

Gráfico 2

Gráfico 3

No gráfico 2 os valores do inner goal e outer goal são respectivamente 202 e 170. No gráfico 3 os valores são 202 e 142. O desvio padrão dos gráficos 2 e 3 é respectivamente 27.8 e 111.1. Comparando com a figura 5.8 a performance não está boa devido ao alto desvio padrão dos gráficos. A explicação para o alto desvio padrão é a grande diferença entre o inner goal e outer goal, é notado que uma menor diferença (32 no gráfico 2 contra 60 no gráfico 3) implica em uma drástica redução do desvio padrão.

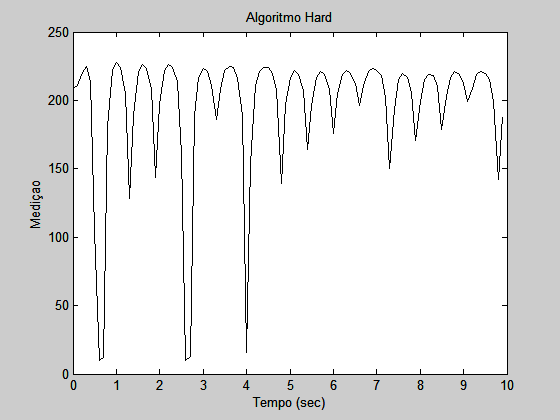
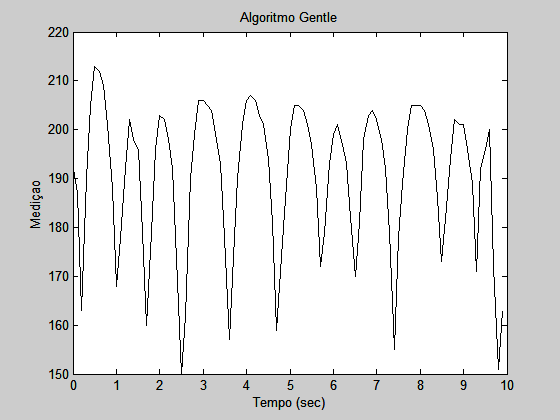
2 – Comparando as figuras 5.5 e 5.7 do livro, o algoritmo gentle-turn oferece desvios mais devagar, provocando menores variações na direção do robô e na leitura do sensor, pois a correção aplicada no motor é menor. Esse algoritmo é bom se o robô sempre permanecer próximo ao goal estabelecido. Já o algoritmo hard-turn oferece desvios mais rápidos, provocando maiores variações na direção do robô e na leitura do sensor. Esse algoritmo é indicado para situações em que o ângulo entre a direção de leitura do sensor e a parede aproximar-se de 0°, pois o hard-turn pode ser capaz de corrigir a direção do robô antes que ele colida com a parede. Os gráficos de medição para os algoritmos hard-turn e gentle-turn são visualizados nos gráficos 4 e 5. O goal para ambos os gráficos é 213. Como era esperado o desvio padrão do hard-turn (48.41) é maior que o desvio padrão do gentle-turn (14.94).

Gráfico 4

Gráfico 5

3 - O algoritmo de três estados pode ser implementado tanto como gentle ou abrupt turn quando trata-se de cornering. As vantagens do algoritmo de três estados é que entre os thresholds, o robô anda reto, cubrindo a maior distância em menos tempo. Os outros algoritmos, durante todo o tempo, corrigem a direção do robô e por isso, andam zigue-zagueando o objetivo, cobrindo a mesma distância que o 3-state em mais tempo.Comparando os desvios padrão o melhor resultado é apresentado pelo gentle-turn, porém caso a diferença de thresholds no algoritmo de 3 estados fosse pequena, este algoritmo provavelmente apresentaria menor desvio padrão.

Em relação a cornering ability, o gentle-turn é viável caso o robô esteja sempre próximo do goal. Ou seja, se a parede fizer uma curva muito abrupta (45° ou mais), o gentle-turn pode não ser capaz de realizar a correção a tempo de evitar a colisão com a parede. Já o hard-turn é viável exatamente na situação oposta. Caso o robô esteja sempre próximo ao goal, o hard-turn irá gerar muita oscilação na direção do robô. Caso o robô tenha que realizar curvas muito fechadas, o hard-turn será capaz de fazer as correções antes que o robô colida com a parede.

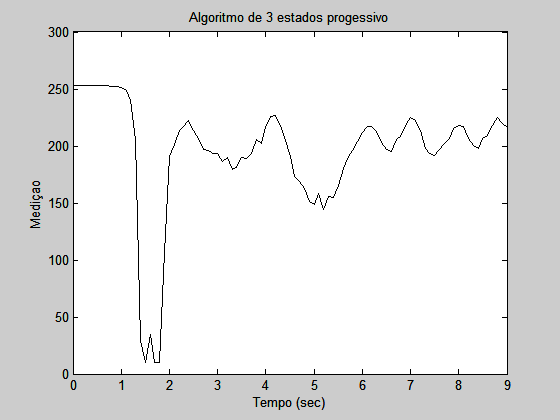
4 - Na implementação das funções left() e right() a potência passada através da função motor() depende dos goals inner e outer além do valor atual de medição do sensor. Quanto maior a diferença entre o valor atual de medição e os setpoints mais abruptas serão as curvas.

O desempenho do algoritmo é visualizado no gráfico 6. O experimento teve o inner goal com valor de 157 e outer goal com valor de 215.

Gráfico 6

No início do experimento (0 a 1 segundo) o robô é colocado distante da parede e por isto os valores iniciais são grandes. O robô começa a se movimentar e como a diferença entre o valor lido pelo sensor e o goal é grande, ele realiza uma grande correção na direção. Isso faz com que o robô chegue bem próximo a parede no momento seguinte e inicie outra correção (instante próximo a 2 segundos). No intervalo de tempo de 2 a 6 segundos o robô ainda apresenta certa oscilação decorrente da sua posição inicial, que por fim se estabiliza. As oscilações a partir desse ponto justificam-se pelo fato do motor da direita (motor mais próximo a parede) gerar mais potência que o da esquerda, fazendo com que o robô desviasse a sua trajetória reta para a esquerda, afastando-se da parede. Vale a pena observar também as variações “constantes” entre o instante 6s e 10s, que mostram que o robô atingiu o estado de andar “reto” e não está mais corrigindo a sua direção, nem causando grandes mudanças na leitura do sensor.

Tarefa 3:

Seção 5.2.3 Exercícios

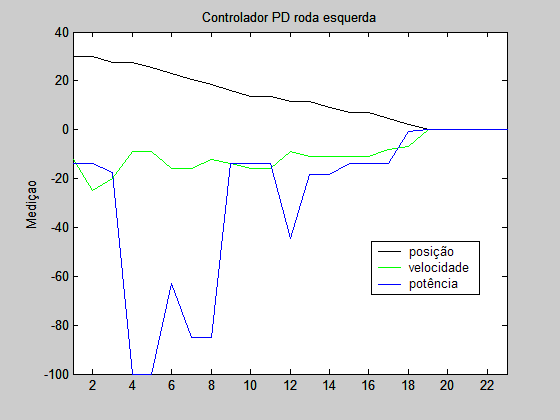
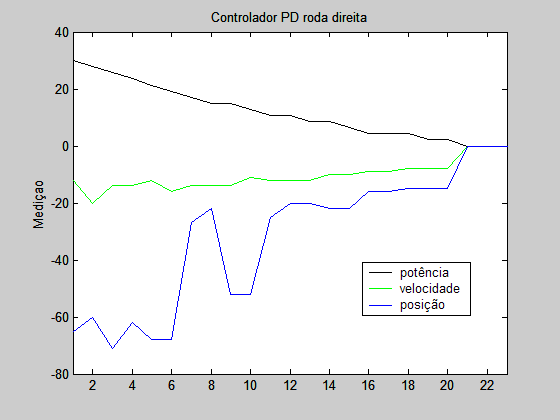
1 – Os gráficos 7 e 8 mostram respectivamente o controlador PD implementado no robô para as rodas esquerda e direita, respectivamente.

Gráfico 7

Gráfico 8

A técnica usada para determinar os ganhos foi a tentativa e erro. O ganho proporcional é igual a 5 e o ganho derivativo é igual a 7. A posição inicial nos gráficos 7 e 8 é equivalente a 30.

4 – O comando de potência é baseado na descrição do livro sendo a combinação da proporção do erro e da velocidade do robô.

Problemas:

As rodas têm diâmetro elevado resultando em um erro grande. O encaixe não perfeito das engrenagens. O robô se deslocando em uma curva mesmo fornecendo a mesma potência para ambos os motores.

O algoritmo usado para o wavefront foi o disponibilizado no site da especificação do trabalho. Para usá-lo foi necessário criar-se duas funções: moverPd e getKnob. Sendo a primeira responsável pelo deslocamento do robô e a segunda para receber entrada do usuário.

Notamos que a implementação não funcionava se chamada mais de uma vez na mesma execução. A solução dada para o problema foi limpar o conteudo da pilha, as variáveis de indice, posicionamento e mapa.

Para implementar a função moverPd utilizamos controle proporcional derivativo (PD). Nosso objetivo era fazer com que o robô se movesse o mais reto possível e que andasse as distâncias exigidas pelo wavefront (no nosso caso utilizamos um grid de espaços 20×20 cm). Apesar de ir reto o suficiente, o robô não fez uma curva tão boa quanto o esperado. Parte do problema talvez seja nossa modelagem PD, parte também foi devido a imprecisão que tinhámos na leitura do sensor, que lia apenas 6 pulsos em uma roda de 25cm perimetro.

Para o próximo trabalho pretendemos aprimorar o controle PD e substituir as rodas de 25cm de perimetro por uma menor. Apesar de não funcionar perfeitamente, o robô é capaz de andar sobre as células, mesmo que com algum erro. Dessa forma, um robô mais próximo do ideal pode ser acalçado com pequenas modificações ao robô e ao algoritmo.

Pegamos o wavefront do site do verlab. Criamos a função moverPd e getKnob, necessárias ao wavefront. Por enquanto a HandyBoard estava sendo carregada e todos do grupo estavam muito atarefados com diversos trabalhos para a semana seguinte.

Hoje os integrantes do grupo estavam menos atarefados, por isso tivemos tempo para ligar os sensores e fazer os testes preliminares com relação ao controle PD.

A construção do robô continua. Continuamos testando com parâmetros para ajustar o shaft-encoder, debugamos o wavefront e começamos a fazer os exercícios a serem entregues que exigem recolhimento de dados.

No final temos o wavefront pronto, grande parte dos exercícios feitos e boas ideias para o controle PD.

Tivemos problemas com os shaft encoders e depois de duas mudanças de posições e dois shaft encoders quebrados, compramos mais shaft encoders e decidimos que eles ficariam no eixo das rodas. Pior para o erro, melhor para a implementação. Os outros eixos em que tentamos colocar os shaft encoders rodavam muito rápido para os sensores, o que impossibilitava uma leitura correta.

Terminamos o controle PD e o robô está pronto para a apresentação. O controle não ficou muito bom por conta desse erro da roda ser muito grande, no entanto, foi a melhor solução que pudemos alcançar em tão pouco tempo.

A apresentação foi pior que os resultados que o robô apresentou no dia anterior. Tivemos problemas com a bateria que não estava 100% e todas as calibragens feitas no dia anterior via código, não ficaram muito boas. Tentamos corrigir esses problemas usando a calibragem do menu, mas mesmo assim o resultado não foi muito favorável.

De qualquer jeito, agora é esperar a competição para ver!